ПИД Регулятор

Программа регулятор

Цифровой регулятор - это программа, которая управляет некоторым процессом (регулирует). Получая входные данные с датчиков, она рассчитывает управляющее воздействие, обычно это некоторое число, которое в итоге с помощью электронной схемы преобразуется в реальное физическое воздействие. Задача регулятора — выйти на заданные показатели датчиков.

Допустим некий прибор на основе микроконтроллера должен регулировать температуру жала паяльника. К прибору подключён датчик температуры жала, который точно показывает текущую температуру жала — T_тек. Ну а пользователь прибора задаёт нужную температуру жала Т_зад , которую прибор и должен поддерживать. Вот типичная задача регулирования. Попробуем самостоятельно придумать программу регулятор температуры жала для этого прибора.

Самое простое, что приходит в голову каждому, это включать паяльник когда заданная температура больше текущей и выключать когда меньше. Данный регулятор очень простой, он получает на входе текущую температуру паяльника, заданную температуру и возвращает число 1 (включить) или 0 (выключить паяльник). Далее микроконтроллер преобразует это число в высокий или низкий уровень напряжения на выводе и управляет паяльником. Это и есть программа регулятор - вполне рабочий вариант. Посмотрим какие у него есть минусы.

Так как прибор цифровой, то все в нем работает по «часам». Датчик температуры выдаёт данные только через какой-то интервал времени. Пусть это будет один раз в секунду. Теперь опишем свойства самого паяльника. При включении паяльника на полную мощность он нагревается за одну секунду на 20 градусов, а остывает за 1 сек на 5 градусов. В таком случае, температура паяльника будет колебаться около заданной +/- 20 градусов.

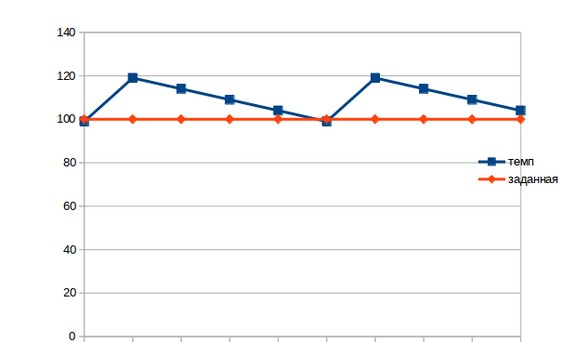
Почему так происходит? Как только мы включим паяльник, через одну секунду он добавит 20 градусов к своей температуре, ещё до того как мы узнаем, что эта самая температура превысила заданную. А потом будет долго остывать. Чтобы сделать реакцию паяльника более плавной, нужно управлять не просто включением его на полную мощность, а иметь возможно регулировать эту мощность. И вот тут как раз и нужен будет ПИД регулятор.

ПИД регулятор

Пусть наш прибор может регулировать мощность паяльника (например с помощью ШИМ модуляции) дискретно (с шагом в 1) в диапазоне от 0 до 10 единиц. 0 — выключен, 10 включён на полную мощность. Теперь, вместо обычного включения паяльника мы можем включить его с некоторой мощностью. Вопрос какая мощность нужна? ПИД регулятор как раз и служит для того, чтобы ответить на этот вопрос. Эта программа автоматически рассчитает нужную мощность в каждый момент времени. Как расшифровывается аббревиатура ПИД:

• П — пропорциональный

• И — интегральный

• Д — дифференциальный

Мощность которую нужно приложить к паяльнику в текущий момент времени складывается из трёх вышеперечисленных компонент. ПИД регулятор находит её автоматически. Разберём что это за компоненты, и как работает алгоритм.

Напомним, что в цифровой электронике нет непрерывных процессов, любая программа выполняется не мгновенно, а за какое-то количество тактов. Датчики выдают данные тоже с некоторой периодичностью. И ПИД регулятор тоже будет работать дискретно. Будем считать (и это очень важно), что программа регулятор вызывается строго через одинаковые промежутки времени (например, каждые 300мс) и вычисляет нужное управляющее воздействие.

Из чего состоит ПИД регулятор

Первый, он же самый простой и понятный компонент — это «П». Он так и называется «пропорциональный». Как он работает?

Пусть у нас есть T_тек и Т_зад. Теперь вычтем одно из другого, получим ошибку E. Задача ПИД регулятора привести эту ошибку к 0. На выходе вычислений как раз и получается нужная мощность с которой должен работать паяльник. Итак, если у нас только один компонент, то будет такая формула:

П = E * K_pgain ; P =

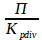
P — рассчитанная мощность, K_pgain * Е — пропорциональный компонент, K_pgain — пропорциональный коэффициент, а K_pdiv — коэффициент делитель. В целочисленной арифметике, удобной для микроконтроллеров, лучше использовать два коэффициента, которые оба целочисленные. Из этой формулы следует, что чем большую ошибку видит регулятор, тем большую мощность он подаёт на паяльник, чтобы быстрее уменьшить ошибку. Таким образом, если паяльник заметно остыл, то он будет включён на полную мощность, а по мере приближения к заданной температуре, регулятор будет подавать все меньшую мощность. Если производить измерения очень быстро и регулировать мощность тоже очень быстро, например 1000 раз в секунду или 10 000, то остальные коэффициенты будут не нужны и будет достаточно одной П компоненты. В таком диапазоне времени все нелинейные процессы становятся линейными. А вот если как у нас — раз в секунду, то они понадобятся.

Следующий компонент — И — интегральный. Он вычисляется чуть сложнее:

И = И + K_igain * Е ;

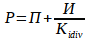
«И» компонент потому и называется интегральный, что по сути он накапливает, интегрирует, ошибку. Как мы предположили ранее, регулятор вызывается строго через равные промежутки времени dt. Поэтому, можно сказать, что K_igain содержит делитель 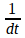. То есть получается, что «И» компонент отражает скорость изменения ошибки. Если процессы у нас линейные (как в нашем паяльнике) и заданная температура постоянна, то «И» в долгосрочной перспективе отражает ту мощность, при которой скорость нагрева паяльника равна скорости его остывания (что нам и нужно). «П» компонент долгосрочно будет стремиться к нулю, а в краткосрочной перспективе, будет учитывать мгновенные изменения во внешней среде. Например, если мы начали паять, паяльник стал остывать быстрее. «П» компонент отреагирует сразу.

Но у нас есть ещё третий компонент «Д». Он является производной скорости изменения ошибки, то есть отражается ускорение нагрева паяльника. Конечно, у паяльника оно равно 0, и этот компонент здесь не имеет смысла (но в других системах он очень важен, например в квадрокоптере), но все равно рассмотрим как он вычисляется. Пусть E_i-1 — ошибка посчитанная на предыдущем шаге, а Е_{i —} текущая ошибка. Тогда «Д» будет вычисляться так:

Д =

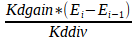
«Д» является как бы тормозом, когда мы «перелетели» через заданную температуру. Когда ещё скорость изменения ошибки положительная, «Д» уже станет отрицательным и быстрее вернёт паяльник к заданной температуре, дополнительно уменьшая рабочую мощность.

Как рассчитать коэффициенты ПИД регулятора

Коэффициенты K_pgain, K_igain K_dgain (параметры ПИД регулятора) находятся опытным путём в процессе настройки регулятора и не меняются в процессе дальнейшей работы регулятора. ПИД регулятор отлично выполняет свою работу, однако, только тогда, когда регулируемая система не меняется. Например, в случае с паяльником, если мы дополнительно начнём охлаждать жало, то настроенный ПИД регулятор перестанет работать, так как дополнительное охлаждение потребует изменения коэффициентов настройки регулятора. Это нужно запомнить. В случае изменения динамической модели управляемой системы, требуется перенастроить параметры ПИД регулятора.

Как же можно подобрать коэффициенты опытным путём? Начнём с коэффициента K_pgain. Его подобрать проще всего. Будем постепенно увеличивать его пока система не начнёт колебаться около заданной температуры. Далее будем уменьшать K_pgain значение пока колебания не уменьшаться. Вот это значение и будет самым оптимальным.

Чтобы подобрать K_igain нужно чуть уменьшить подобранный ранее коэффициент K_pgain . При этом ошибка станет положительной, мы будем не догонять заданную температуру. Вот в это время и начинаем увеличивать K_igain . «И» начнет интегрировать ошибку повышая мощность, пока опять не начнутся колебания. Они уже будут значительно меньше, чем в случае с одним коэффициентом.

«Д» подобрать сложнее. Нужно резко (импульсно) менять заданную температуру и смотреть, чтобы температура паяльник не «перелетала» заданную. Увеличивая K_dgain мы исключим «перелёты».

Как запрограммировать ПИД регулятор

Программируется ПИД регулятор на удивление просто.

Любой регулятор на языке программирования это функция, которая получает в качестве параметров данные датчиков и возвращает вычисленное значение управляющего воздействия. Сразу приведём пример типичной функции ПИД регулятора, а потом разберём как она работает и посмотрим как её использовать в реальном приборе на базе микроконтроллера.

s16 PID_Regulator(s16 hReference, s16 hPresentFeedback,PPID_Struct_t PID_Struct)
{
  s32 wError, wProportional_Term,wIntegral_Term, houtput_32;
  s32 wIntegral_sum_temp; 
  s32 wDifferential_Term;
 
  // error computation
  wError= (s32)(hReference - hPresentFeedback);
 
  // Proportional term computation
  wProportional_Term = PID_Struct->pPID_Var->hKp_Gain *wError;
 
  // Integral term computation
  if (PID_Struct->pPID_Var->hKi_Gain == 0)
  {
    PID_Struct->pPID_Var->wIntegral = 0;
  }
  else
  { 
    wIntegral_Term = PID_Struct->pPID_Var->hKi_Gain *wError;
    wIntegral_sum_temp = PID_Struct->pPID_Var->wIntegral +wIntegral_Term;
 
    if (wIntegral_sum_temp > 0)
    {
      if (PID_Struct->pPID_Var->wIntegral < 0)
      {
        if (wIntegral_Term < 0)
        {
          wIntegral_sum_temp = S32_MIN;
        }
      }
    }
    else
    {
      if (PID_Struct->pPID_Var->wIntegral > 0)
      {
        if (wIntegral_Term > 0)
        {
          wIntegral_sum_temp = S32_MAX;
        }
      }
    }    
 
    if (wIntegral_sum_temp >PID_Struct->pPID_Const->wUpper_Limit_Integral)
    {
      PID_Struct->pPID_Var->wIntegral =PID_Struct->pPID_Const->wUpper_Limit_Integral;
    }
    else if (wIntegral_sum_temp <PID_Struct->pPID_Const->wLower_Limit_Integral)
    { 
      PID_Struct->pPID_Var->wIntegral =PID_Struct->pPID_Const->wLower_Limit_Integral;
    }
    else
    {
      PID_Struct->pPID_Var->wIntegral = wIntegral_sum_temp;
    }
  }
  // Differential term computation
  {
  s32 wtemp;
 
  wtemp = wError - PID_Struct->pPID_Var->wPreviousError;
  wDifferential_Term = PID_Struct->pPID_Var->hKd_Gain *wtemp;
  PID_Struct->pPID_Var->wPreviousError = wError;    // storevalue 
  }
 
  houtput_32 =(wProportional_Term/PID_Struct->pPID_Const->hKp_Divisor+ 
               PID_Struct->pPID_Var->wIntegral/PID_Struct->pPID_Const->hKi_Divisor+ 
               wDifferential_Term/PID_Struct->pPID_Const->hKd_Divisor); 
 
  if (houtput_32 > PID_Struct->pPID_Const->hUpper_Limit_Output)
  {
    houtput_32 = PID_Struct->pPID_Const->hUpper_Limit_Output;              
  }
  else if (houtput_32 <PID_Struct->pPID_Const->hLower_Limit_Output)
  {
    houtput_32 = PID_Struct->pPID_Const->hLower_Limit_Output;
  }
  return((s16)(houtput_32));     
}
 

Кажется сложным. Но на самом деле это не так. Начнём с определения функции. Функция принимает три параметра. hReference — заданное значение, hPresentFeedback — текущее значение с датчика и третий параметр структура с настройками конкретного объекта ПИД регулятора. Таким образом, функция может обслуживать сразу несколько ПИД регуляторов.

wError= (s32)(hReference — hPresentFeedback);
wProportional_Term = PID_Struct->pPID_Var->hKp_Gain *wError;
 

Вычисляем ошибку wError, и сразу считаем пропорциональную составляющую wProportional_Term. Все нужные коэффициенты находятся в структуре. Все вычисления производим в целочисленной системе, умножения в начале, а все деления в конце кода (для этого повышаем разрядность вычислений до 32 бит).

  if (PID_Struct->pPID_Var->hKi_Gain == 0)
  {
    PID_Struct->pPID_Var->wIntegral = 0;
  }
  else
  { 
    wIntegral_Term = PID_Struct->pPID_Var->hKi_Gain *wError;
    wIntegral_sum_temp = PID_Struct->pPID_Var->wIntegral +wIntegral_Term;
 

Далее считаем интегральный компонент. Если интегральный коэффициент равен нулю, то и вычислять нечего — интегральный компонент равен нулю. Накопленное значение интегральной компоненты храним в структуре «PID_Struct→pPID_Var→wIntegral». И добавляем туда опять же целую часть коэффициента умноженного на ошибку.

    if (wIntegral_sum_temp > 0)
    {
      if (PID_Struct->pPID_Var->wIntegral < 0)
      {
        if (wIntegral_Term < 0)
        {
          wIntegral_sum_temp = S32_MIN;
        }
      }
    }
    else
    {
      if (PID_Struct->pPID_Var->wIntegral > 0)
      {
        if (wIntegral_Term > 0)
        {
          wIntegral_sum_temp = S32_MAX;
        }
      }
    }    
 

Теперь нужно разобраться с переполнением этого компонента. Заметим сразу, что типы здесь все знаковые — ошибка может быть как положительной, так и отрицательной. Очень важно корректно все сделать с точки зрения целочисленной математики ограниченных типов.

В этой части кода обрабатывается ситуация, когда к максимальному положительному числу для выбранной разрядности прибавили положительное число, то результат станет отрицательным! Это надо отследить и ограничить результат максимальным положительным числом. То же самое для отрицательной части.

    if (wIntegral_sum_temp >PID_Struct->pPID_Const->wUpper_Limit_Integral)
    {
      PID_Struct->pPID_Var->wIntegral =PID_Struct->pPID_Const->wUpper_Limit_Integral;
    }
    else if (wIntegral_sum_temp <PID_Struct->pPID_Const->wLower_Limit_Integral)
    { 
      PID_Struct->pPID_Var->wIntegral =PID_Struct->pPID_Const->wLower_Limit_Integral;
    }
    else
    {
      PID_Struct->pPID_Var->wIntegral = wIntegral_sum_temp;
    }
 

Иногда бывает полезно сразу ограничить интегральную составляющую некими заранее известными лимитами. Например, у нас итоговая мощность лежит в интервале от 0 до 10. То и интегральный компонент не должен выходить за эти приделы (естественно после деления). Ну и в итоге нужно результат положить в структуру в интегральный компонент, его надо запомнить на следующий раз.

  {
  s32 wtemp;
 
  wtemp = wError - PID_Struct->pPID_Var->wPreviousError;
  wDifferential_Term = PID_Struct->pPID_Var->hKd_Gain *wtemp;
  PID_Struct->pPID_Var->wPreviousError = wError;    // storevalue 
  }
 

Теперь считаем дифференциальный компонент. Коэффициент умножаем на разницу текущей ошибки и предыдущей. После этого предыдущую ошибку заменяем на текущую.

  houtput_32 =(wProportional_Term/PID_Struct->pPID_Const->hKp_Divisor+ 
               PID_Struct->pPID_Var->wIntegral/PID_Struct->pPID_Const->hKi_Divisor+ 
               wDifferential_Term/PID_Struct->pPID_Const->hKd_Divisor); 
 
  if (houtput_32 > PID_Struct->pPID_Const->hUpper_Limit_Output)
  {
    houtput_32 = PID_Struct->pPID_Const->hUpper_Limit_Output;              
  }
  else if (houtput_32 <PID_Struct->pPID_Const->hLower_Limit_Output)
  {
    houtput_32 = PID_Struct->pPID_Const->hLower_Limit_Output;
  }
  return((s16)(houtput_32));     
 

И финальный подсчёт с учётом делителей всех трёх компонент. Возвращаем полученное значение мощности.

Пользоваться такой процедурой очень легко. Вызывать её нужно строго с одинаковой периодичностью, лучше с помощью прерываний по таймеру. А далее уже можно делать какие-либо управляющие действия.

Лучше сразу все коэффициенты (кроме делителей) делать в виде переменных, чтобы можно было быстро и легко настроить регулятор в процессе отладки. Коэффициенты можно менять либо через UART, либо с помощью ADC и переменного резистора или пошагово с помощью кнопок. А ещё это удобно делать сразу через программатор в режиме отладки кода. Напрямую с компьютера.

Тема ПИД регулятора очень объёмная, в интернет можно найти очень много статей посвящённых этому виду регулятора. На этом мы закончим знакомство с ним и перейдём к реальным приборам — паяльная станция. В этом приборе его и задействуем.